Algebra 2
Page: 3 of 5
Solving Quadratic Equations
Quadratic equations have a degree of two and contains only one variable. When plotted the quadratic equation has a parabola shape. The coefficient of the x2 variable determines the orientation of the graph. The parabola shape has a turning point called a vertex which is either the maximum or minimum of the graph. The parabola shape also has an axis of symmetry parallel to the y-axis through the vertex.
Graphical Methods
If the quadratic equation has real roots then the points where the curve crosses or touches the x-axis are the roots of the equation.
Algebraic Methods
- Factorising
Find the factors of the quadratic equation and then solve each factor to find the roots.
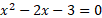
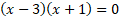
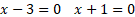

- Quadratic Root Formula
This formula is used to find the roots of the equations directly. This formula is used when the roots are not integers.
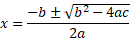
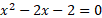
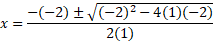
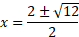
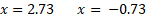
- Completed Square Form
The quadratic equation can be solved by converting it into completed square form which can be solved directly to find the roots.
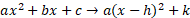
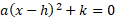
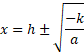
Example One
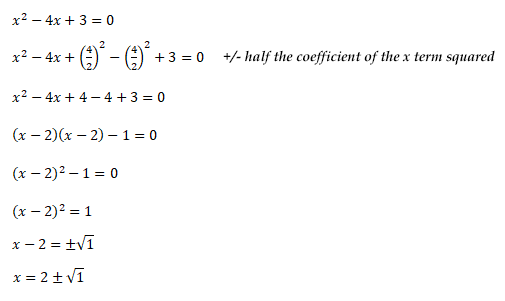
Example Two
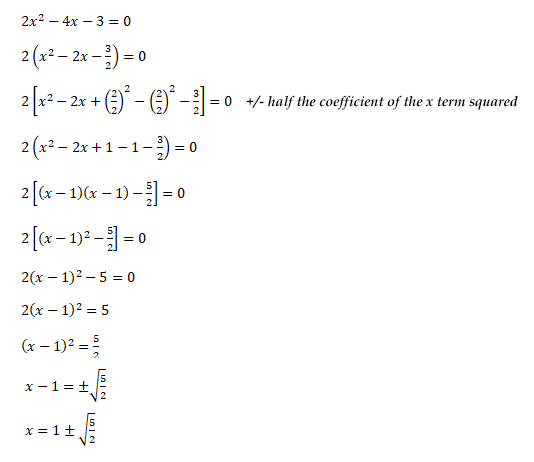
- Substitution
This method is used when the quadratic equation is in a complex form.
Example